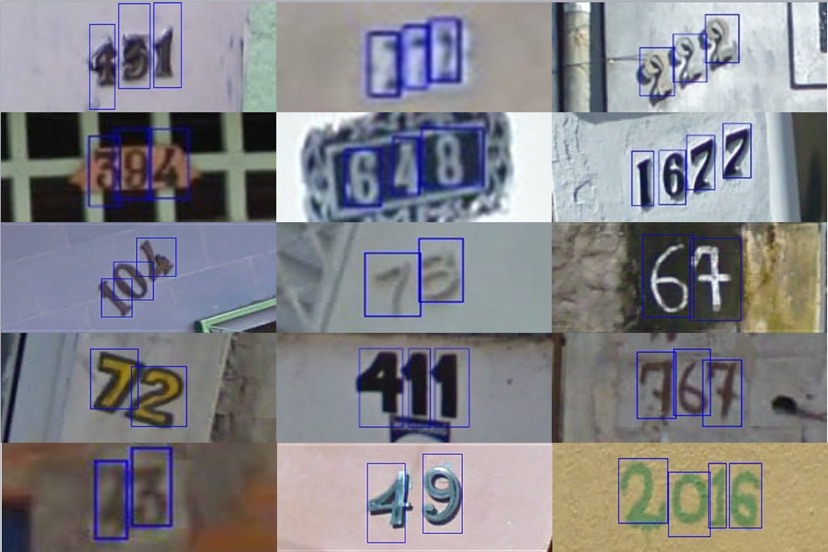Python实现10大经典排序算法
大家好,我最近在重学数据结构与算法这门课,顺手整理了10大经典排序算法的Python实现,并配有动画加以理解,建议收藏起来慢慢食用~
好了,废话少说,上干货 !
1. 冒泡排序
123456def bubbleSort(arr): for i in range(1, len(arr)): for j in range(0, len(arr)-i): if arr[j] > arr[j+1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] return arr
2. 选择排序
1234567891011def selectionSort(arr): for i in range(len(arr) - 1): # 记录最小数的索引 minIndex = i for j in range(i + 1, len(arr)): if arr[j] < arr[minIndex]: ...
SinGAN
飞船驶过梵高的星空
大雁掠过夕阳,留下惊鸿一瞥
乌云蔽日,草木涌动
是不是很炫酷?
其实,比这更酷的是:仅使用一张图片便可实现以上所有效果,甚至更多。
这一切的背后,都是SinGAN的功劳。
ps:不想看原理的小伙伴可以划到本文最后一部分,直接动手实现这些好玩的操作,起飞~
SinGAN介绍
SinGAN由多个不同尺度的生成器和判别器组成,如上图所示。对于每一个尺度,都会进行一次与普通GAN训练类似的训练过程。
具体地,从下往上看:
在最开始训练时,当前尺度的生成器$G_N$接受噪声$Z_N$,输出生成图像$\widetilde{x}_N$;然后将$\widetilde{x}_N$与真实图像下采样得到的$x_N$一起输入判别器$D_N$,$D_N$负责判别输入图像是真实的还是生成的;(对应图中倒数第一行)
在第二次训练时,当前尺度的生成器$G_{N-1}$接受两个东西:噪声$Z_{N-1}$和上一阶段生成的$\widetilde{x}N$的上采样结果,输出生成图像$\widetilde{x}{N-1}$;然后将$\widetilde{x}{N-1}$与真实图像下采样得到的$x{N-1} ...
街景字符编码识别
本文属于学习帖,用于记录“街景字符编码识别”问题的 baseline 解决方案。原代码链接见文末,其中有些小的错误已更正。
赛题来源自Google街景图像中的门牌号数据集(The Street View House Numbers Dataset, SVHN),并根据一定方式采样得到比赛数据集。
训练集数据包括3W张照片,验证集数据包括1W张照片,每张照片包括颜色图像和对应的编码类别和具体位置;测试集A包括4W张照片,测试集B包括4W张照片。
本赛题需要选手识别图片中所有的字符,为了降低比赛难度,我们提供了训练集、验证集和测试集中字符的位置框。
一个比较有效的方法是先对字符做检测(使用目标检测技术),但这里仅使用baseline方案。
baseline解决方案是将其转为定长字符识别问题。
具体来说,所有字符的最大长度不超过6位,因此将不足6位的字符填充到6位。因为所有字符全部取值为0到9共10个数字,所以用10作为填补的标记,字符总长度不足6位的样本用10进行填补。
导入相关库+必要设置1234567891011121314151617181920212223import numpy ...
ProGAN
ProGAN的结构ProGAN也是用于图像生成的一种生成对抗网络。在原始GAN 以及一些GAN变体中,都是对搭建好的整个网络(包括生成器和判别器)直接进行训练。而ProGAN的独特之处在于采用了逐步增长的方式,如下图所示:
具体来说,生成器最开始只有一层,用于生成分辨较低的图像,比如图中的44;此时判别器也只有一层,将生成的44的图片和真实的4*4的图片一起输入到判别器进行,得到输出结果。训练若干轮次。
接下来,给生成器加一层,使得其生成的图像分辨率可以高一些,比如图中的88;此时也给判别器加一层,将生成的88的图片和真实的8*8的图片一起输入到判别器,得到输出结果。训练若干轮次。
一直重复上述过程,直到生成器生成的图像分辨率达到指定大小。
从上述描述可以看出,对于每一个特定层数的网络来说,其训练过程和原始GAN以及一些GAN变体的训练过程是一样的。ProGAN的精髓就在于它的网络(生成器和判别器)是逐步增长的。
下面这张动态图演示了上述文字描述的过程:
ProGAN的细节描述淡入我们已经说过,生成器和判别器的训练不是一蹴而就的,而是逐步增长的。而且,对于训练好的网络层,当新的层来临时 ...
Transformer
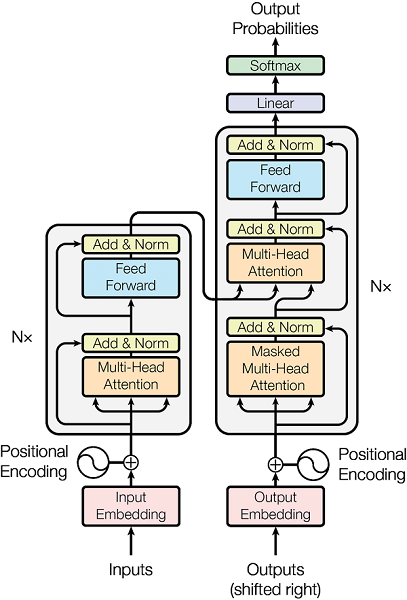
Transformer的结构Transformer的结构如上图所示,我们将其拆解为x个小部分,逐个部分用代码实现,然后再将各个部分联结起来,形成最终的Transformer。
关于Transformer的原理,网上已经有很多优质的文章了,这里我们关心其代码实现。对于其每一个子模块(以类的形式定义),我们都会实例化一个对象,用具体的数值代入其中,把中间过程中产生的变量维度及相关信息打印出来,这些都体现在代码注释中,请留意。
Muti-Head AttentionMuti-Head Attention接收输入q,k,v,维度在这里都是$[4,3,512]$,输出维度也是$[4,3,512]$。
q和k的维度是一致的,而v可以和它们不一致,这里只是为了方便才将三者维度保持一致。
SelfAttention实现代码如下 (注意注释)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707 ...
CycleGAN
上图中,最左边一列是原图,右侧的4列是将原图转换成其他风格后的图像。这种转换被称为图像风格迁移。
实现图像风格迁移的方法有很多,这里我们介绍CycleGAN并用它来实现图像风格迁移。
CycleGAN的网络结构CycleGAN的网络结构如上图所示。它的训练数据集需要来自两个不同的域(就是两种不同风格的图像):$A,B$;
CycleGAN包含两个生成器:$G_{AB},G_{BA}$,分别用于将A风格图像转换为B风格图像,以及将B风格图像转换为A风格图像;
同样,它也包含两个判别器:$D_{A},D_{B}$。
CycleGAN的损失函数在原始GAN损失函数的基础上,CycleGAN为了防止生成器偷懒(解释见下一段),增加了循环一致性损失,这个东西其实就是重构损失,以保证转换后的图像和原图像的内容一致性。
李宏毅老师的PPT中一幅图很形象的展示了循环一致性损失
现在举个例子解释偷懒 的含义:比如由A风格转换为B风格时,需要把转换后的图像(记作$B_{fake}$)与真实的B风格图像(记作$B_{real}$)一起喂入判别器$D_B$,而$D_B$只是希望$B_{real}$与真实B风 ...
从GAN到WGAN再到WGAN-GP
之前介绍了GAN的原理,并使用celeba数据集训练了一个基于DCGAN的”假”人脸生成器(传送门戳我),这里我把它的生成效果图搬运过来了在GAN问世后,其出色的表现使得对于GAN的研究一时风生水起(至今还在持续),越来越多关于GAN的研究成果被发表,GAN本身存在的缺陷也逐步被挖掘出来。
本文不会陷入繁杂的数学推导中,而是指出WGAN相比于原始GAN的改进之处,以及进一步提出的WGAN-GP,并动手用PyTorch进行实现。
WGANWGAN便是对于原始GAN的一种改进方案,它的作者用了大量篇幅指出了原始GAN的不足之处,并最终给出了自己的解决方案。虽然其中蕴含了大量的数学推导,但推导的结论却出乎意料的简单,或许这就是数学的魅力。
说完一堆废话后,来看看改进得到的WGAN相比于原始GAN有哪些改动,这里直接把WGAN作者给出的训练算法贴出来,然后做简要分析。
5和10分别给出了判别器和生成器的损失函数,相比于原始GAN 的损失函数,仅仅是去掉了log。如果不能一下子看出来,可以把原始GAN的目标函数搬过来对比下。
原始GAN的优化目标:
其中的E代表期望,由大数定律,我们可以用均值近 ...
火爆全球的GAN究竟是何方神圣?
故事时间从前有一个人,他希望通过制造假币来发家致富。
于是,他开始学习制造假币。
一开始,他的技术太菜,制作的假币刚流入市场就被警察发现了。
他不甘心,于是继续学习来提升造假币技术,这一次,假币并没有被发现,他很开心的数着钱。
可是,过了一段时间,敏锐的警察使用刚刚学习到的新知识,破获了他的假币。
但他还是不甘示弱,继续提升造假币的技术
警察也继续学习新的假币鉴别技术
就这样,他的造假币技术一直在提升,警察鉴别假币的技术也在不断提升
在互相抗衡很久以后,他的造假币技术到了炉火纯青的地步,以至于警察都难以鉴别。
GAN是什么?
生成对抗网络(Generative adversarial network, GAN)由生成器(一般用$G$表示)和判别器(一般用$D$表示)组成,常用于生成”假”的东西,比如假的文本,假的人脸图像等等,本文以图像生成为例进行叙述。
生成器负责将从某分布中随机采样的噪声$z$通过神经网络映射为”生成图像”$G(z)$;判别器负责鉴定给定的图像是真实图像$X$还是生成器生成的图像$G(z)$。
在上面的故事中,警察充当着判别器$D$的角色,而造假币的人充当着生成器$ ...
变分自编码器
Vae他有一些烦恼反正现在的年轻人都有许多烦恼那么多要思考那么多要寻找诱惑太多 不坚定就犯错了
哦哦,不对,不是这个Vae,也不是uae~
是接下来出场的VAE~
对比AE,引出VAE之前介绍了自编码器(AE)的原理(传送门),当时讲到自编码器并不具有真正的生成能力,以图像为例来说,它只能将输入的图像$X$编码成隐向量$z$,然后将$z$作为解码器的输入,得到输出图像$X’$。如果我们尝试将与$z$的shape一致的”随机特征表示”输入解码器,那么得到的将是毫无意义的噪声图像。
变分自编码器(VAE)突破了这一限制!
先给出结论:在VAE中,只要随机特征表示(这里也将这些特征表示记作$z$)是从某些分布,如标准正态分布中采样得到的,那么将$z$输入解码器之后可以得到与训练集图像类似但不同于训练集中任何一张图像的新图像。
比如,训练集是手写数字图像,那么在训练完成后,将从标准正态分布中采样得到的$z$输入解码器,可以得到一些新的手写数字图像。
以上所说的特征表示$z$,被称为隐向量(latent vector)。
VAE究竟是如何做到这一点的呢?且往下看。
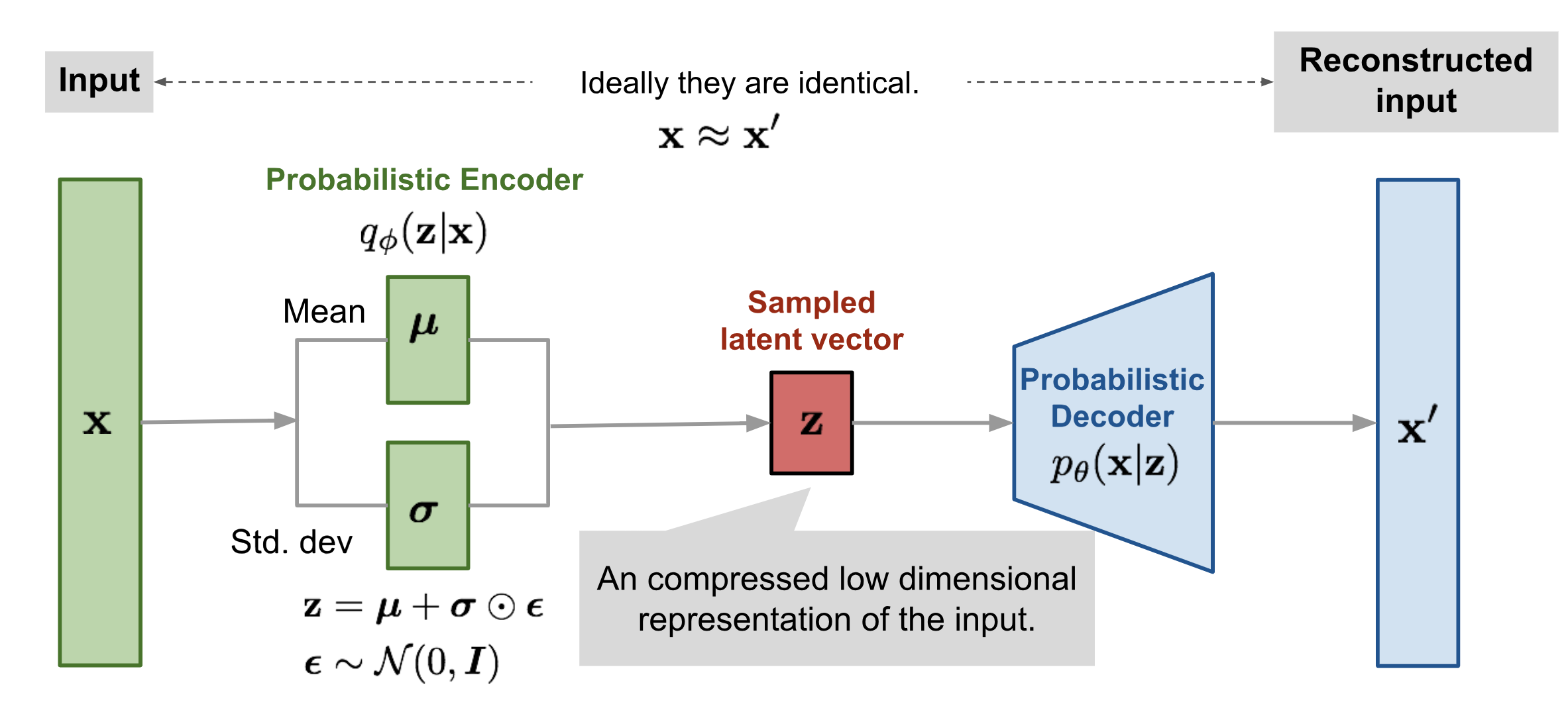
VAE的结构
变分自编码 ...
自编码器
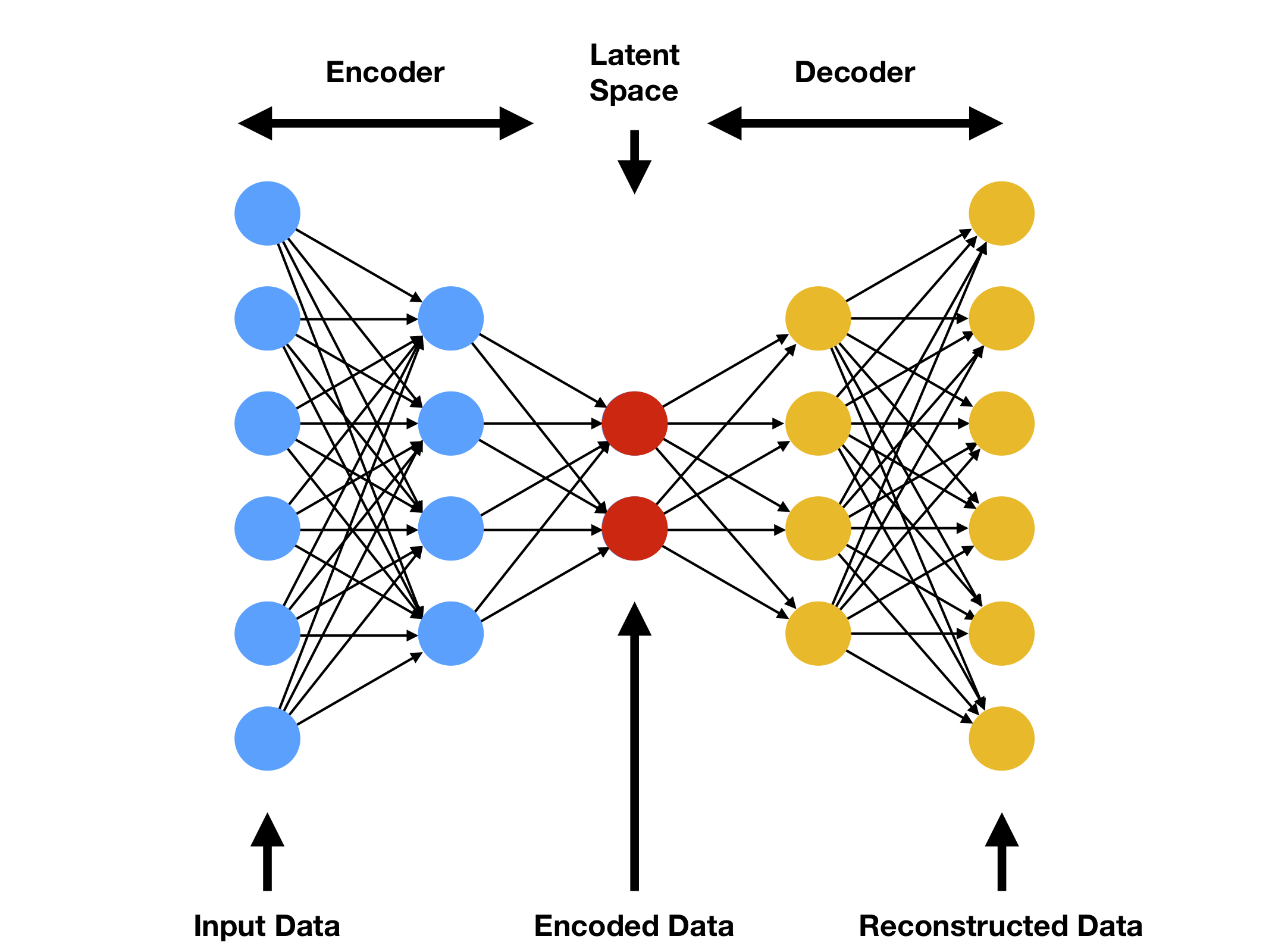
自编码器的结构自编码器(Auto Encoder)是一种神经网络模型。它由两部分组成:编码器(Ecoder)和解码器(Decoder)。
编码器用于将输入数据(Input Data)进行编码,从而将输入数据映射到维度较低的隐空间(Latent Space),得到被编码的数据(Encoded Data)。
解码器用于将隐空间中被编码的数据还原(解码)成”输入数据”。这里之所以打引号,是因为还原得到的”输入数据”相比于一开始的输入数据来说会有一些损失,所以并不是真正意义上的输入数据。
下图展示了自编码器的结构
自编码器的应用数据降维/特征提取从自编码器的结构很容易想到它的这一用途。在训练阶段,$X$经过编码器映射得到低维的$z$,$z$通过解码器还原出与$X$维度一致,内容相似的$X’$,通过反向传播来更新网络权重,以最小化输入$X$与输出$X’$之间的损失。
其中的$z$便是降维后的数据,因为如果可以通过$z$还原出输入$X$,那么可以说$z$已经学习到了$X$的大部分特征。
同时,$z$是一个被高度压缩(降维)的输入数据的表示,所以也可以将自编码器看作一个特征提取器,提取到的 ...