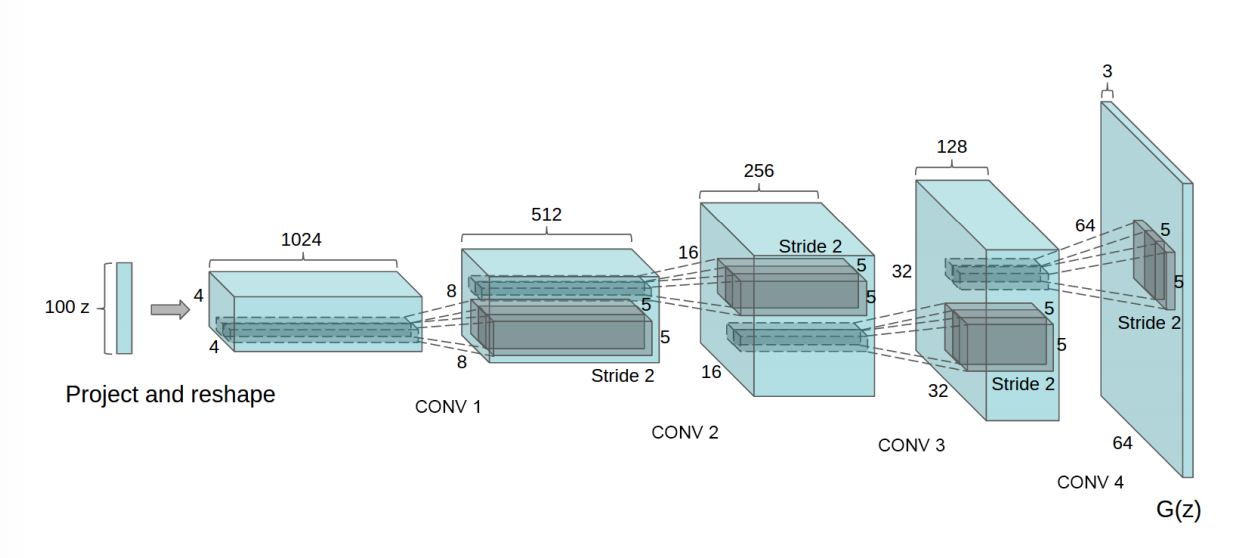
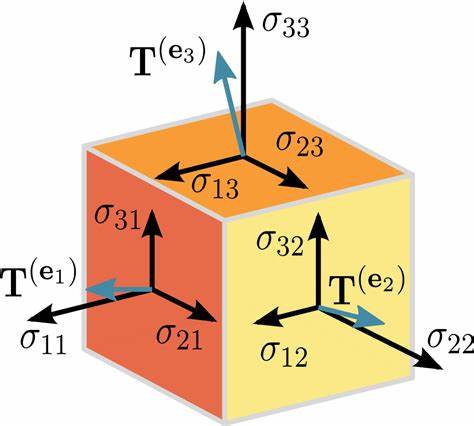
对前面三篇文章的总结
序章起初,我觉得使用Keras的那些API,比如train_on_batch,compile等等,极大的减少了代码量,对刚刚入门的小白来说比较友好。
在开始接触GAN之后,发现一些关于GAN的书籍,比如GANs in action,一些关于GAN的博客,如machinelearningmastery,CSDN以及一些能搜到的视频教程,很多都是用的Keras或者tf.keras
于是我也准备学习用tf.keras来实现各种GAN。
后来,经过一小段时间的学习,虽然也跟着别人的代码写出了几个能跑通的GAN,但总觉得keras的代码怪怪的。
高度封装的API,虽然容易使得小白入门,但同时也使得使用者对其内部的机制还是不怎么了解。比如之前困扰我很久的一个问题,就是关于模型的trainable参数的设置问题,明明已经设置为discriminator.trainable=False了,在后面的train_on_batch时,discriminator还能被训练。最后找到了一个不太确定的答案,详细见这篇文章:
https://fx0809.gitee.io/2020/10/12/Keras%E4%B ...
DCGAN_V2.0
导入相关函数1234import tensorflow as tfimport matplotlib.pyplot as pltimport numpy as npfrom tensorflow.keras import layers
准备数据1(train_images,train_labels),(_,_)=tf.keras.datasets.mnist.load_data()
1train_images.shape
1train_images.dtype
1train_images=train_images.reshape(train_images.shape[0],28,28,1).astype('float32')
1train_images.shape
1train_images.dtype
1train_images=(train_images-127.5)/127.1#归一化
12BATCH_SIZE=256BUFFER_SIZE=60000
1datasets=tf.data.Dataset.from_tensor ...
【警告原因不明,怀疑是梯度消失】warning:tensorflow:Grandients_do_not_exist
更新!!!
好像并不是Dropout的原因,在训练SGAN时也出现了同样的警告,即使已经设置了Dropout层的traing=True,怀疑是梯度消失(有文章说是这个 https://www.jiqizhixin.com/articles/2018-11-27-24 )或爆炸
在本文中,可能设置training=Trur恰好避免了梯度消失或爆炸,只是凑巧而已(猜测)
具体原因后续再来分析,先这样了。
问题提出基于DCGAN(https://fx0809.gitee.io/2020/10/07/DCGAN/)的代码,想要将生成器和判别器的实现方式改为继承自`tf.keras.Model`类的方式,修改部分的代码如下:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869class Generator_model(tf.keras.Model): def __init__(sel ...
【训练结果很糟糕】SGAN
2020年10月16号更新:
应该是由于判别器本身的网络结构导致的(应证了猜想1)。
在训练ACGAN时,梯度也出现了问题(warning),我将判别器由卷积层换成了全连接层,再次运行就能正常训练了,详见这篇文章:
什么是SGAN在原始GAN架构的基础上,将判别器的二分类(真实样本or生成样本)改为多分类(共N+1,N classes+fake),便得到了SGAN( Semi-Supervised GAN) 。
此时,分类器(同时也是判别器)的表现更好,并且生成器生成的图片的质量也更高。
如何实现SGAN生成器模型无需改动,需要改动的是判别模型以及后续的训练过程
导入相关函数12345import tensorflow as tfimport matplotlib.pyplot as pltimport numpy as npfrom tensorflow.keras import layersfrom tensorflow.keras.utils import to_categorical
准备数据1(train_images,train_labels),(_,_)=tf.ke ...
Keras中关于模型的trainable状态的问题
提出问题在看GAN的实现代码的时候,发现了这么一个地方:
123456789101112131415161718192021222324252627282930313233class GAN(): def __init__(self): self.img_rows = 28 self.img_cols = 28 self.channels = 1 self.img_shape = (self.img_rows, self.img_cols, self.channels) self.latent_dim = 100 optimizer = Adam(0.0002, 0.5) # Build and compile the discriminator self.discriminator = self.build_discriminator() self.discriminator.compile(loss='binary_crossentropy& ...
CDCGAN
和CGAN一样,只是采用了卷积层替换全连接层的方法来搭建生成器和判别器的网络
导入所需函数12345678910import tensorflow as tffrom tensorflow import kerasfrom tensorflow.keras import layersfrom tensorflow.keras.layers import Input,multiply,Flatten,Embeddingfrom tensorflow.keras.models import Modelimport matplotlib.pyplot as pltimport numpy as npimport globimport osfrom tensorflow.keras.utils import to_categorical
准备数据1(train_images,train_labels),(_,_)=tf.keras.datasets.mnist.load_data()
1train_images.shape
(60000, 28, 28)
1train_ ...
CGAN
什么是CGAN所谓CGAN,就是在GAN的基础上,多施加了一些条件信息,比如图像的标签等,使得生成器可以按照我们指定的标签去生成所对应的图像。
普通GAN的目标函数为:
而CGAN的目标函数为:
CGAN的网络结构如下:
如何构建CGAN本文在普通GAN(全连接层搭建)的基础上,将生成器的输入由“噪声”改为“噪声+对应该批次图像的真实标签”,将判别器的输入由”图像”改为”图像+对应该批次图像的真实标签”,最后在测试生成器的生成能力时,人为构建了0到9这10个数字作为标签(因为训练数据是mnist数据集),和随机噪声一起喂入生成器以产生新的图片。
Tensorflow2.0 实现CGAN导入所需函数12345678910import tensorflow as tffrom tensorflow import kerasfrom tensorflow.keras import layersfrom tensorflow.keras.layers import Input,multiply,Flatten,Embeddingfrom tensorflow.keras.models i ...
tf.keras.layers.Embedding
函数原型1tf.keras.layers.Embedding(input_dim, output_dim, embeddings_initializer='uniform', embeddings_regularizer=None, activity_regularizer=None, embeddings_constraint=None, mask_zero=False, input_length=None, **kwargs)
举个图像数据的例子这里的input_shape是(10),output_shape是np.prod((28, 28, 1))
1234567from tensorflow.keras.layers import multiply,Flatten,Embeddingimg=tf.ones((2,28,28,1))#两张图片label=np.array([1,2])#两个标签label_embedding = Flatten()(Embedding(10, np.prod((28, 28, 1)))(label))flat_im ...
FrechetInceptionDistance
什么是FIDFréchet Inception Distance (FID) 度量了真实图片和生成图片在 feature 层面的距离
FID越小,则图像多样性越好,质量也越好
众所周知,预训练好的神经网络顶层可以提取图片的高级信息,一定程度能反映图片的本质。因此,FID 的提出者通过预训练的 Inception V3 来提取全连接层之前的 2048 维向量,作为图片的特征。 具体的做法是:去掉最后的输出层( 最后一层是一个pooling层,原来的网络通过该pooling层可以输出一张图像的类别 ),然后得到一个2048维的高层特征,这个高层特征是一个长向量形式。
FID的计算公式如下:
在这里,将每一张图片输入分类器中,都会得到一个2048维的长向量,对所有图片得到的长向量求平均值,求协方差矩阵,就得到了公式中的四个部分的值。
FID 只把 Inception V3 作为特征提取器,并不依赖它判断图片的具体类别,因此不必担心 Inception V3 的训练数据和生成模型的训练数据不同。同时,由于直接衡量生成数据和真实数据的分布之间的距离,也不必担心每个类别内部只产生一模 ...
InceptionScore
IS使用两个标准来衡量GAN的性能:
The quality of the generated images, and
their diversity.
熵可以看作是对随机性的度量。如果随机变量x的值是高度可预测的,则其熵较低。相反,如果它是高度不可预测的,那么熵就很高。例如,在下图中,我们有两个概率分布p(x)。p2具有比p1更高的熵,因为p2具有更均匀的分布,所以更难以预测x。
质量在GAN中,我们希望条件概率*P(y | x)*具有高度可预测性(低熵),比如红色线表示的分布。
(Images that are classified strongly as one class over all other classes indicate a high quality. As such, the conditional probability of all generated images in the collection should have a low entropy. )
即给定一张图像,我们应该容易地知道对象的类型。因此,我们*使用Inception网 ...